Моделювання лінійних пружних матеріалів - наскільки це складно?

1. Ізотропна лінійна пружне середовище
2. Модуль Юнга, модуль зсуву і коефіцієнт Пуассона
3. Модуль об'ємної пружності
4. параметри Ламі
5. Нестисливі лінійних пружних матеріалів
6. Ортотропія і анізотропія
7. геометрична нелінійність
8. Заключні зауваження по лінійним пружним матеріалами

Наши партнеры ArtmMisto

Найбільш основоположною моделлю матеріалу в механіці суцільних середовищ є модель лінійної пружною середовища. Як не банально це звучить, але деякі важливі особливості цієї моделі можуть бути не очевидні з першого погляду. У даній статті ми заглибимося в теорію і прикладні аспекти застосування цієї моделі середовища і дамо уявлення про изотропии і анізотропії, допустимих значеннях властивостей матеріалів, несжимаемости і вплив геометричної нелінійності.

Ізотропна лінійна пружне середовище

У переважній більшості випадків при моделюванні, що включає застосування лінійних пружних матеріалів, мають справу з ізотропної середовищем, пружні властивості якої не залежать від напрямку. Для опису такого матеріалу потрібно лише два незалежні параметри, що визначають властивості матеріалу. Існує багато різних способів вибору цих параметрів, однак деякі з них більш популярні, ніж інші.

Модуль Юнга, модуль зсуву і коефіцієнт Пуассона

Модуль Юнга, модуль зсуву і коефіцієнт Пуассона - найбільш часто зустрічаються в таблицях параметри, що описують пружні властивості матеріалів. Вони не є незалежними, так як модуль зсуву, G, пов'язаний з модулем Юнга, E, і коефіцієнтом Пуассона, \ nu, співвідношенням

G = \ frac {E} {2 (1 + \ nu)}

Модуль Юнга може бути безпосередньо виміряно в експерименті по одноосьовому розтягування, тоді як модуль зсуву вимірюється, наприклад, в експерименті чистого кручення.

Крім цього, при одноосьовому розтягуванні коефіцієнт Пуассона визначає, наскільки матеріал буде сідати (або, можливо, розширюються) в поперечному напрямку. Допустимий діапазон значень становить -1 <\ nu <0.5, де позитивні значення вказують на те, що матеріал стає тоншою при розтягуванні. Є кілька матеріалів, які називаються ауксетики , Які мають негативний коефіцієнт Пуассона. Пробка у винній пляшці має коефіцієнт Пуассона близький до нуля, так що її діаметр практично не змінюється незалежно від того, витягають її або проштовхують.

Для багатьох металів і сплавів \ nu \ approx 1/3, і модуль зсуву, таким чином, становить близько 40% від модуля Юнга.

З урахуванням можливих значень \ nu допустимі значення відносини модуля зсуву до модуля Юнга лежать всередині інтервалу

\ Frac {1} {3} <\ frac {G} {E} <\ infty

Коли значення \ nu наближається до 0.5, матеріал стає нестисливим. При аналізі таких матеріалів виникають специфічні проблеми, які ми обговоримо нижче.

Модуль об'ємної пружності

Модуль об'ємної пружності, K, визначає зміна обсягу при заданому рівномірному стисненні. Виражений через E і \ nu, він запишеться у вигляді:

K = \ frac {E} {3 (1-2 \ nu)}

Коли \ nu = 1/3, значення модуля об'ємної пружності дорівнює значенню модуля Юнга, але для нестисливого матеріалу (\ nu \ to 0.5), K прагне до нескінченності.

Модуль об'ємної пружності зазвичай задається разом з модулем зсуву. Ці дві величини є, в деякому сенсі, більш фізично незалежними параметрами. Зміна обсягу матеріалу визначається тільки модулем об'ємної пружності, тоді як спотворення його форми - тільки модулем зсуву.

параметри Ламі

Параметри Ламі (коефіцієнти Ламі, константи Ламі, постійні Ламі, пружні постійні Ламі, модулі пружності Ламі) \ mu і \ lambda в основному використовуються для математичного опису явищ пружності. Повна система 3-х мірних матеріальних співвідношень між тензором напружень \ boldsymbol \ sigma і тензором деформацій \ boldsymbol \ varepsilon (в разі однорідноїізотропної пружного середовища) може бути записана в компактній формі за допомогою параметрів Ламі у вигляді:

\ Boldsymbol \ sigma = 2 \ mu \ boldsymbol \ varepsilon + \ lambda \; \ Mathrm {trace} (\ boldsymbol {\ varepsilon}) \ mathbf I

Параметр \ mu є просто модулем зсуву, тоді як параметр \ lambda може бути представлений як

\ Lambda = \ frac {E \ nu} {(1+ \ nu) (1-2 \ nu)}

Повну таблицю перетворень між різними пружними параметрами можна подивитися тут .

Нестисливі лінійних пружних матеріалів

Деякі матеріали, такі як, наприклад, гума, є практично нестисливими. З математичної точки зору повністю нестисливий матеріал принципово відрізняється від стискання. В силу того, що відсутня зміна обсягу, тепер не представляється можливим визначити середню напругу. Рівняння стану для середньої напруги (тиску), p, як функції зміни обсягу, \ Delta V, у вигляді

p = f (\ Delta V)

більше не існує, і замість цього воно повинно бути замінено на обмеження, що констатує, що

\ Delta V = 0

Інший підхід до проблеми несжимаемости випливає з факту, що член (1-2 \ nu) з'являється в знаменнику матеріальних рівнянь, так що поділ на нуль може статися тільки за умови \ nu = 0.5. Чи не спробувати, в такому випадку, змоделювати нестисливий матеріал приблизно, встановивши значення \ nu = 0.499?

Це можна зробити, але в даному випадку, стандартне зміщення вузлів сітки, отримане на основі формалізму методу скінченних елементів, може призвести до несподіваних результатів. Це викликано явищем, званим блокування. Можливі ефекти:

• надмірно жорсткі моделі;
• «Шахова» картина напружень;
• повідомлення про помилки або попередження від решателя про поганої обумовленості системи рівнянь.

Корекція результатів можлива при використанні змішаної формулювання, в якій тиск вводиться в якості додаткової міри свободи. У середовищі COMSOL Multiphysics, включити змішану формулювання можна, вибравши пункт Майже нестисливий матеріал в налаштуваннях моделі матеріалу.

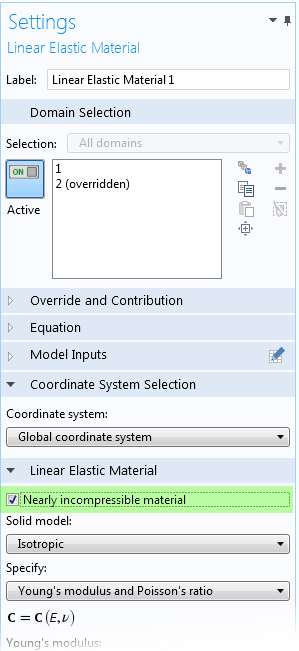
Частина налаштувань моделі лінійного пружного матеріалу, з підтримкою змішаної формулювання.

При величині коефіцієнта Пуассона більшою, ніж 0,45 (але, природно, не більшою 0,5), або коли модуль об'ємної пружності більш ніж на порядок перевищує модуль зсуву, доцільно використовувати змішану формулювання. Ефект від її використання показаний на малюнку нижче.

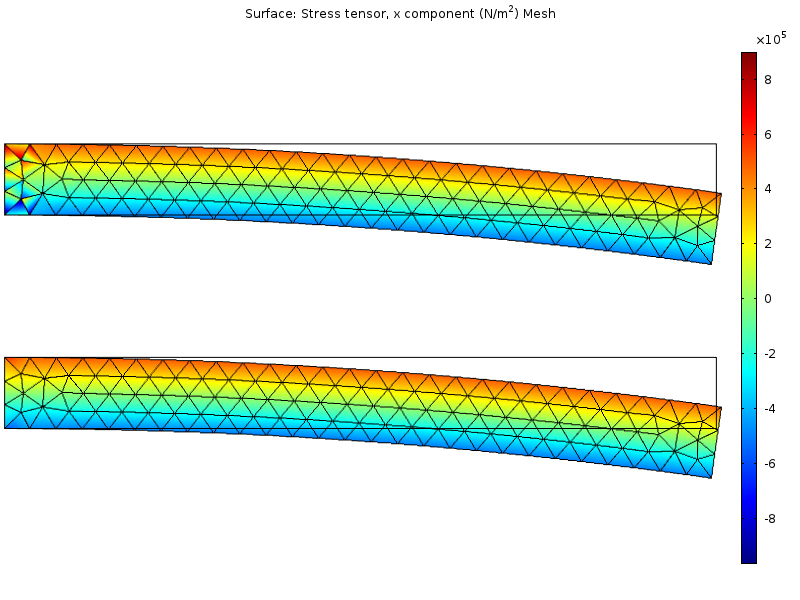
Розподіл напружень в простій моделі плоских деформацій, \ nu = 0.499. Верхнє зображення показує рішення, засноване на стандартній формулюванні, тоді як нижня відноситься до змішаної формулюванні.

У рішенні, яке використовує в якості ступенів свободи тільки зміщення вузлів, картина розподілу напружень виявляє спотворення в лівій частині, де є обмеження. Ці спотворення практично повністю усуваються при використанні змішаної формулювання.

Ортотропія і анізотропія

У загальному випадку властивості лінійних пружних матеріалів залежать від напрямку. У найбільш загальному випадку анізотропного матеріалу це означає, що всі шість компонент тензора напружень можуть залежати від усіх шести компонент тензора деформації. Для опису цього потрібно 21 матеріальний параметр. Ясно, що отримання всіх цих даних в експерименті є дуже непростим завданням. Якщо напруга, \ boldsymbol \ sigma, і деформацію, \ boldsymbol \ varepsilon, трактувати як 6-ти мірні вектори (по числу незалежних компонент тензора), вони будуть пов'язані між собою за допомогою 6х6 симетричною матриці матеріальних параметрів \ mathbf D

\ Boldsymbol \ sigma = \ mathbf D \ boldsymbol \ varepsilon

На щастя, як правило, неізотропние матеріали мають певну симетрію. В окремому випадку ортотропного матеріалу, є три виділених ортогональних напрямки, в яких зрушення відділяється від осьового дії. Тобто, розтягування матеріалу уздовж одного з цих головних напрямків, призведе тільки стисненню (без зсуву) в двох інших ортогональних напрямках. Повний опис ортотропного матеріалу вимагає дев'яти незалежних матеріальних параметрів.

Матеріальні співвідношення в ортотропних матеріалі легше сприймаються, коли вони записані у вигляді матриці податливості (зворотної до матриці пружних модулів), \ boldsymbol \ varepsilon = \ mathbf C \ boldsymbol \ sigma:

\ Mathsf {C} =
\ Begin {bmatrix}
\ Tfrac {1} {E _ {\ rm X}} & - \ tfrac {\ nu _ {\ rm YX}} {E _ {\ rm Y}} & - \ tfrac {\ nu _ {\ rm ZX}} {E_ { \ rm Z}} & 0 & 0 & 0 \\
- \ tfrac {\ nu _ {\ rm XY}} {E _ {\ rm X}} & \ tfrac {1} {E _ {\ rm Y}} & - \ tfrac {\ nu _ {\ rm ZY}} {E_ { \ rm Z}} & 0 & 0 & 0 \\
- \ tfrac {\ nu _ {\ rm XZ}} {E _ {\ rm X}} & - \ tfrac {\ nu _ {\ rm YZ}} {E _ {\ rm Y}} & \ tfrac {1} {E_ { \ rm Z}} & 0 & 0 & 0 \\
0 & 0 & 0 & \ tfrac {1} {G _ {\ rm YZ}} & 0 & 0 \\
0 & 0 & 0 & 0 & \ tfrac {1} {G _ {\ rm ZX}} & 0 \\
0 & 0 & 0 & 0 & 0 & \ tfrac {1} {G _ {\ rm XY}} \\
\ End {bmatrix}

Оскільки матриця податливості повинна бути симетричною, то дванадцять незалежних використовуваних параметрів (ненульових компонентів) скорочуються до дев'яти, за допомогою трьох співвідношень симетрії типу

\ Tfrac {\ nu _ {\ rm YX}} {E_Y} = \ tfrac {\ nu _ {\ rm XY}} {E_X}

Зверніть увагу, що \ nu _ {\ rm YX} \ neq \ nu _ {\ rm XY}, тому при роботі з ортотропними даними необхідно бути впевненим в тому, що використовується значення потрібного коефіцієнта Пуассона. У різних джерелах позначення і, відповідно, значення можуть відрізнятися.

Анізотропія і ортотропія зазвичай виникають в неоднорідних матеріалах. Найчастіше ці властивості не вимірюються, а обчислюються за допомогою процесу гомогенізації, коли мікроскопічні властивості масштабируются до макроскопічного рівня. (Суть процесу полягає в усередненні мікроскопічних рівнянь - рівнянь, що описують поведінку і властивості однієї мікрочастинки - по макроскопическому обсягом, виявляючи і зберігаючи при цьому властивості, які характеризують, як індивідуальну мікрочастинок, так і весь ансамбль мікрочастинок в цілому.) Обговорення такої гомогенізації, правда в дещо іншому контексті, можна знайти в даної блог-статті .

Для неізотропних матеріалів можуть бути встановлені обмеження на допустимі значення матеріальних параметрів, аналогічні описаним для ізотропних матеріалів. Скрутно в явному вигляді продемонструвати ці обмеження, але є дві речі, на які варто звернути увагу:

1. матриця матеріальних параметрів \ mathbf D повинна бути позитивно певної;
   1. для довільного анізотропного матеріалу досить перевірити, що всі власні значення матриці позитивно певні величини;
   2. для ортотропного матеріалу це справедливо, якщо всі шість пружних модулів позитивні, і виконується нерівність \ nu _ {\ rm XY} \ nu _ {\ rm YX} + \ nu _ {\ rm YZ} \ nu _ {\ rm ZY} + \ nu _ {\ rm ZX} \ nu _ {\ rm XZ} + \ nu _ {\ rm YX} \ nu _ {\ rm ZY} \ nu _ {\ rm XZ} <1
2. якщо матеріал має низьку сжимаемостью, то необхідно застосовувати змішану формулювання;
   1. для цього можна оцінити ефективний модуль об'ємної пружності і порівняти зі значеннями модулів зсуву;
   2. в разі невизначеності краще перестрахуватися і затратити зайві ресурси на змішану формулювання, щоб уникнути можливих неточностей.

геометрична нелінійність

При вирішенні геометрично нелінійних задач значення терміна "лінійна пружність" в дійсності є питанням угоди. Проблема полягає в тому, що існує кілька можливих уявлень для опису напруг і деформацій. Обговоренню різних заходів деформацій і напружень присвячена попередня блог-стаття .

Так як в якості вихідних величин напруг і деформацій в середовищі COMSOL Multiphysics прийняті другий тензор напружень Піола-Кірхгофа і тензор заходи деформації Гріна-Лагранжа, то природна властивість лінійної пружності полягає в тому, що ці величини мають лінійну залежність один щодо одного. Такий матеріал іноді називають матеріалом Сен-Венана.

Інтуїтивно можна припустити, що термін "лінійна пружність" означає існування лінійної залежності між прикладається силою і зміщенням в простому експерименті по розтягуванню. Однак це не так, оскільки і напруги, і деформації змінюються в міру розтягування. Щоб показати це, розглянемо стрижень з квадратним поперечним перерізом.

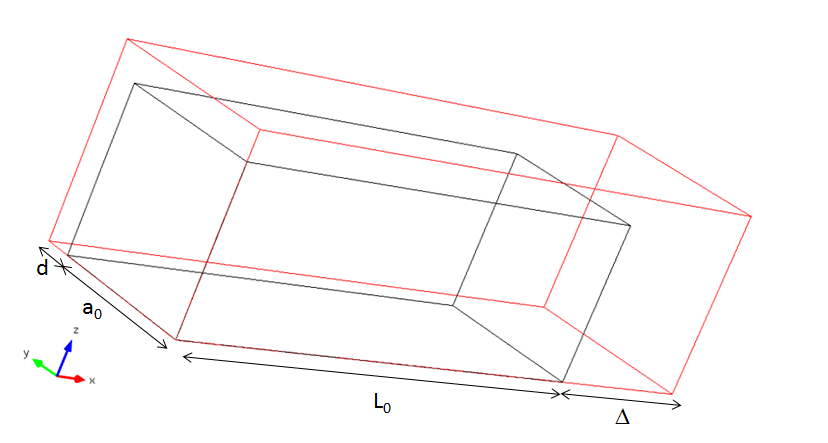
Стрижень, підданий рівномірному розтягування.

Вихідна довжина стрижня дорівнює L_0, і первісна площа поперечного перерізу становить A_0 = a_0 ^ 2, де a_0 - сторона початкового перетину. Припустимо, що стрижень подовжується на величину \ Delta, так що поточна його довжина становить L = L_0 + \ Delta = L_0 (1+ \ xi)

Тут 1+ \ xi - це осьовий розтяг і \ xi можна розглядати як відносне подовження. Нова довжина сторони в поперечному перерізі буде дорівнює a = a_0 + d = a_0 (1+ \ eta), де \ eta - відносне подовження в поперечному напрямку.

Сила може бути виражена через складову тензора напруги Коші \ sigma_x в осьовому напрямку, помножену на поточну площа поперечного перерізу:

F = \ sigma_x A = \ sigma_x A_0 (1+ \ eta) ^ 2

Щоб використовувати лінійну пружну залежність тензорів напруги і деформації, тензор напруження Коші \ boldsymbol \ sigma необхідно висловити через другий тензор напруги Піола-Кірхгофа \ mathbf S за допомогою перетворення виду

\ Mathbf \ sigma = J ^ {- 1} \ mathbf F \ mathbf S \ mathbf F ^ T

де \ mathbf F - тензор градієнта деформації, а масштабування обсягу визначається J = det (\ mathbf F) якобіаном переходу з однієї системи координат в іншу. Опускаючи деталі, для одноосного випадку отримаємо

\ Sigma_x = \ frac {F_ {xX}} {F_ {yY} F_ {zZ}} S_X = \ frac {(1+ \ xi)} {(1+ \ eta) ^ 2} S_X

Так як для матеріалу Сен-Венана при одноосьовому розтягуванні осьове напруження пов'язане з осьової деформацією як S_X = E \ epsilon_X, отримуємо

F = S_x A_0 (1+ \ xi) = E A_0 (1+ \ xi) \ varepsilon_X

З урахуванням того, що осьової член тензора деформації Гріна-Лагранжа визначається виразом

\ Varepsilon_X = \ frac {\ partial u} {\ partial X} + \ frac {1} {2} (\ frac {\ partial u} {\ partial X}) ^ 2 = \ xi + \ frac {1} {2 } \ xi ^ 2

вираз для сили в залежності від зміщення перетвориться до виду

F = E A_0 (1+ \ xi) (\ xi + \ frac {1} {2} \ xi ^ 2) = E A_0 (\ xi + \ frac {3} {2} \ xi ^ 2 + \ frac {1 } {2} \ xi ^ 3)

Ми бачимо, що з урахуванням геометричної нелінійності лінійний пружний матеріал насправді має на увазі кубічну залежність між силою і відносним подовженням (або сили від зсуву, оскільки \ Delta = L_0 \ xi), як показано на малюнку нижче.

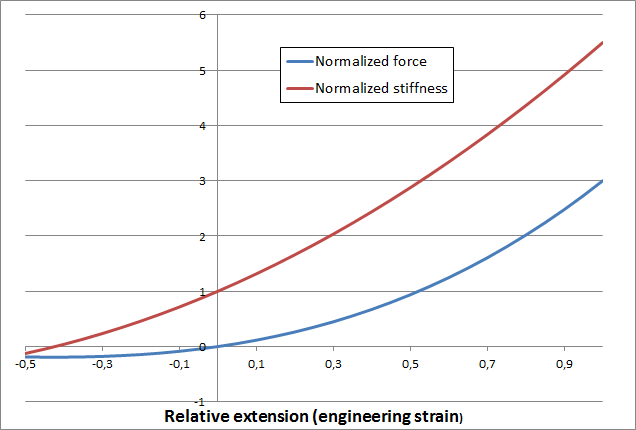
Одноосьовий відгук лінійного пружного матеріалу, обумовлений геометричній нелинейностью.

Як видно з графіка, жорсткість матеріалу прагне до нуля з боку стиснення, \ xi = \ sqrt {{1} / {3}} - 1 \ approx -0.42. На практиці це означає, що моделювання при такому ступені деформації буде безглуздим. Насправді це не є проблемою, так як можна сміливо стверджувати, що не існує реальних матеріалів, які залишаються лінійними при таких великих деформаціях. Однак моделі лінійних пружних матеріалів найчастіше використовуються далеко за межами розумного діапазону напруг з кількох причин, серед яких можна виділити наступні:

• часто потрібно швидко оцінити що-небудь «по порядку величини», перш ніж використовувати більш складну модель матеріалів;
• в моделі є сингулярності, які викликають дуже високі деформації в деяких точках;
  • більш детально про сингулярності можна подивитися тут .
• в дослідженні контактних задач завжди проявляється геометрична нелінійність;
  • часто в ході аналізу високий рівень стискають напруг (а, отже, і деформацій) з'являється локально на якийсь час в зоні зіткнення матеріалів.

У всіх цих випадках вирішувач може не знайти рішення, якщо деформації стиснення стають занадто великими. Якщо ви підозрюєте, що зіткнулися з такою ситуацією, то гарною ідеєю буде графічне побудова найменшого головного значення тензора деформації. Якщо воно менше, ніж -0,3 або близько того, то можна очікувати такого роду збій при моделюванні. Критичним значенням, в термінах деформації по Гріну-Лагранжу, є -1/3. Якщо проблема полягає в цьому, то слід розглянути можливість заміни моделі на відповідну модель гіперпружних матеріалу.

Стиснення - це не єдина проблема. У наведеному вище аналізі коефіцієнт Пуассона не входив в рівняння. Так що ж, насправді, відбувається з поперечним перерізом?

За визначенням, в одноосьовому випадку поперечна деформація пов'язана з осьової за допомогою відносини

\ Varepsilon_Y = - \ nu \ varepsilon_X

Оскільки ці деформації є компонентами тензора деформацій Гріна-Лагранжа, значить вони підкоряються нелінійним виразами

\ Frac {\ partial v} {\ partial Y} + \ frac {1} {2} (\ frac {\ partial v} {\ partial Y}) ^ 2 = - \ nu (\ frac {\ partial u} { \ partial X} + \ frac {1} {2} (\ frac {\ partial u} {\ partial X}) ^ 2)

Таким чином, при деформації є сильна нелінійна залежність у зміні поперечного перерізу. Рішення цього квадратного рівняння приводить до наступного співвідношенню між поперечної і поздовжньої деформаціями

\ Eta = \ sqrt {1 \ nu (\ xi ^ 2 + 2 \ xi)} - 1

Результат показаний на малюнку нижче.

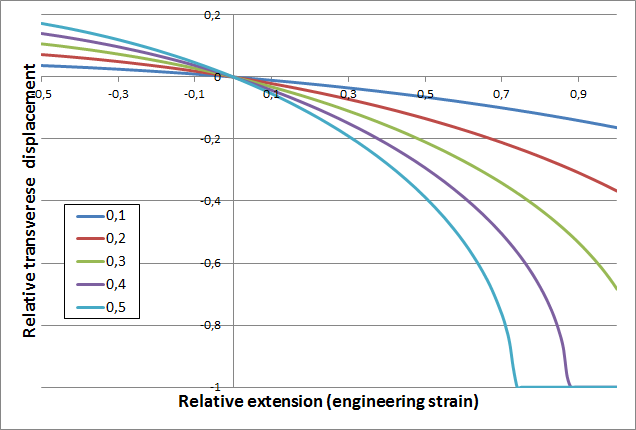
Поперечний зсув як функція осьового зсуву для одноосного розтягу матеріалу Сен-Венана. Показані залежності для п'яти різних значень коефіцієнта Пуассона.

Як видно, поперечний переріз швидко стискається при великих ушкодженнях зі зростанням значень коефіцієнта Пуассона.

Якби був обраний інший спосіб представлення напруги і деформації, наприклад, якби тензор напруги Коші був пропорційний логарифмічною, або "істинної" деформації, то це призвело б, швидше за все, до зовсім іншого результату. Такий матеріал має жорсткість, яка, навпаки, зменшується при подовженні, коли зв'язок між силою і зміщенням визначається значенням коефіцієнта Пуассона. Проте, обидва матеріали можна коректно називати "лінійно пружними", хоча результати обчислень для великих пружних деформацій в рамках двох різних платформ моделювання можуть сильно відрізнятися між собою.

Заключні зауваження по лінійним пружним матеріалами

Ми проілюстрували деякі обмеження на використання лінійних пружних матеріалів. Зокрема, вказали на можливі підводні камені, пов'язані з нестислива, і комбінацією лінійної пружності з великими деформаціями.

Для цікавляться питаннями моделювання матеріалів в будівельній механіці і механіці суцільних середовищ дотримуйтеся таких блог-статтями: