Сонячна система: закони руху.

Наши партнеры ArtmMisto

Закон всесвітнього тяжіння
Перший закон Кеплера
обурення
Другий закон Кеплера
Третій закон Кеплера
Узагальнений третій закон Кеплера
космічні швидкості
узагальнення

У Сонячну систему входять Сонце, дев'ять великих планет, їх супутники, тисячі астероїдів, мільярди комет, незліченна кількість пилинок, крижинок і просто заряджених частинок. Більш детально читайте тут

Закон всесвітнього тяжіння

Майже всі в Сонячній системі обертається навколо Сонця. У деяких планет є супутники, а й вони, здійснюючи свій шлях навколо планети, разом з нею рухаються навколо Сонця. Сонце має масу, яка перевищує масу всього іншого населення Сонячної системи в 750 разів. Завдяки цьому Сонце змушує планети і все інше рухатися по орбітах навколо себе. У космічних масштабах маса є головною характеристикою тіл, тому що всі небесні тіла підкоряються закону всесвітнього тяжіння.

За цим законом, відкритого англійським фізиком Ісааком Ньютоном у другій половині 17-го століття, все тіла, що мають масу, притягуються силою, пропорційною добутку їх мас і обернено пропорційною квадрату відстані між ними. Така взаємодія називають гравітаційним, а силу √ гравітацією. Якщо Ви хоч трохи знайомі з фізикою, Вас не втомить математична формула закону:

Тут F √ сила тяжіння, m 1 і m 2 √ маси двох тіл, R √ відстань між ними, G √ так звана гравітаційна стала. Її значення дорівнює силі, з якою притягуються два тіла масами по 1 кг, рознесені на відстань 1 м. Ця сила невелика, саме тому значення гравітаційної постійної, можливо, здасться Вам маленьким: 6,6720. 10- 11 Н. м 2 / кг 2. Визначити гравітаційну постійну на досвіді з малими тілами вперше вдалося Генрі Кавендишу в 1788-му році. Він вивчав взаємодію свинцевих куль діаметром 5 і 20 см.

Ми не помічаємо того, що, скажімо, дві людини гравітаційно притягуються між собою. Якщо люди і тягнуться один до одного, то фізикою цього не пояснити. Однак досліди з визначення сили, з якою притягуються підвішений вертикально вантаж і величезна скеля провести цілком можливо. Гравітація √ сила, яка стає помітною для великих мас.

Не впадаючи в ще одну поширену помилку, яке полягає в твердженні, що при взаємодії двох тіл різних мас тяжче діє на легке тіло з більшою силою, ніж легке діє на важке. Це не вірно. Сили, з якими діють один на одного два тіла, однакові. Подивіться на формулу. У будь-якому випадку маси тел перемножуються.

Але Ви запитаєте, чому ж тоді планеті не обертатися разом з Сонцем, скажімо, навколо Землі, адже сила, з якою діє Земля на Сонце, дорівнює силі, з якою Сонце діє на Землю. Це так, сили рівні. Але дія цих сил по-різному. Штовхніть ногою м'яч. А потім з тією ж силою вдарте по бетонному блоку. Як то кажуть, відчуйте різницю. Однієї і тієї ж сили достатньо для того, щоб зрушити Землю, але її ж не вистачить для того, щоб помітно потурбувати Сонце. Маси у них різні. Коли камінь падає на Землю, він підкоряється закону всесвітнього тяжіння. Він теж діє на Землю, але її рух назустріч каменю мізерно мало. Тому ми говоримо, що камінь падає на Землю.

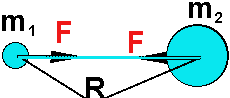Тепер зупинимося на тому, в якому напрямку діє сила гравітації. Ця сила додається до одного з взаємодіючих тіл і спрямована в бік іншого. До цього іншого прикладена така ж по величині сила, але вона спрямована в бік першого. Сили спрямовані по прямій лінії, що з'єднує взаємодіючі тіла. А якщо т ак, тоді чому ж все в Сонячній системі не падає на Сонце?

Все обов'язково потрапляло б на Сонце, якби це все стояло на місці. Діюча сила намагається змінити швидкість тіла, прагнучи її розгорнути у напрямку сили. Кидаючи камінь, ми зауважимо, що той не падає у наших ніг, а описує в повітрі криву лінію. Сила тяжіння поступово змінила напрямок і величину швидкості каменю, і той впав на деякій відстані від нас. Чим більшу швидкість ми повідомимо каменю, кидаючи його, тим довше доведеться гравітації міняти напрям швидкості, тим далі від нас камінь вдариться об Землю. А тепер згадаємо про те, що Земля не плоска, а кругла. Що якщо ми з такою силою кинемо камінь, що за кожну секунду гравітація буде наближати його до Землі на таку ж відстань, на яке крива поверхня Землі буде йти від каменю? В такому випадку камінь буде рухатися по колу навколо Землі, не падаючи на неї. Цей рух буде відбуватися під дією сили гравітаційного тяжіння. Камінь буде намагатися летіти в бік від Землі, а гравітація з таким же запалом буде прагнути викривити шлях каменю в сторону поверхні. До такого висновку, зокрема, прийшов І. Ньютон в своєму уявному киданні каменів з високої гори. Отже, Сонце викривляє рух планет, не даючи їм розлетітися в різні боки.

закони Кеплера

1.
Орбіти планет являють собою більш складні фігури, ніж окружність. Ще в кінці 16-го століття, на початку 17-го (тобто до відкриття Ньютоном закону всесвітнього тяжіння) Йоганн Кеплер вперше зважився переглянути причини руху планет навколо Сонця, Місяця навколо Землі. Він помилявся в оцінці природи притягує сили, але здогадувався, що Сонце спотворює тяжінням шляху планет, які прагнуть рухатися по прямій. Кеплер на основі результатів кропітких і багаторічних спостережень Тихо Браге за планетою Марс зміг визначити форму його орбіти. Після тривалих розрахунків, помилок, розчарувань, перебору безлічі варіантів (математика не давала в той час можливості йти іншим шляхом), Кеплер досяг узгодження своїх результатів і записів про спостереження датського астронома. Орбіта виявилася еліпсом. Сонце Кеплер розташував в одному з фокусів еліпса. Таким чином, з'явився перший емпіричний (тобто виведений зі спостережень) з АКОН Кеплера: будь-яка планета рухається по орбіті у вигляді еліпса, в одному з фокусів якого знаходиться Сонце. Падаючий на землю після нашого кидка камінь до моменту падіння описує в повітрі траєкторію, яка є малою частиною еліпса, в одному з фокусів якого знаходиться центр Землі.

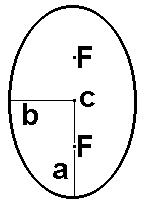Еліпс - геометрична фігура, властивість якої полягає в тому, що сума відстаней від будь-якої точки еліпса до двох особливих точок, іменованих фокусами еліпса (F), є величиною постійною. У еліпса ще виділяють точку центру (С). Основним же поняттям для цієї фігури є ексцентриситет. Ексцентриситет - параметр, який є характеристикою витягнутості еліпса. Він дорівнює відношенню відстані від центру еліпса до його фокуса до довжини велика піввісь (a) або стосовно кореня з різниці квадратів великої і малої (b) піввісь до довжини велика піввісь:

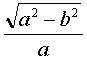
Ексцентриситет позначається латинською буквою е. Аналіз формул дає нам знати, що для кола (а = b) ексцентриситет дорівнює нулю. Інші значення цієї величини визначають разомкунтие криві. Для параболи (а нескінченно велике) ексцентриситет дорівнює одиниці. Ексцентриситет, більший, ніж одиниця, описує гіперболу.

Треба сказати, що в разі планет відміну орбіт від кіл невелика (е несильно відрізняється від нуля). Значну витягнутість мають лише орбіти Меркурія (е = 0,206) і Плутона (е = 0,25). Орбіти астероїдів і комет можуть мати різну витягнутість. Кометні орбіти часто мають як параболічну, так і гіперболічного форму. Під гравітаційною дією планет комети іноді спотворюють свій шлях, прискорюються або сповільнюються. Результатом цього і може послужити сильне зміна форми орбіти.

Згадаймо також, що гравітаційна взаємодія притаманне всім тілам, які мають масами. Через це орбіти всіх тіл Сонячної системи постійно змінюються: все планети діють один на одного. Така дія (мале, в порівнянні з дією Сонця) називають возмущающим. А зміни в шляху небесних тіл √ збуреннями. Наприклад, обурює сила гравітаційного тяжіння Юпітера значно змінює орбіти астероїдів. Дія на Місяць Землі і Сонця роблять абсолютно непридатними для розрахунків її орбіти закони Кеплера.

2.
Вивчаючи за спостереженнями закономірності руху планет, Кеплер зміг відкрити і таке правило: за будь-які рівні проміжки часу лінія, що з'єднує Сонце з планетою, покриває рівні за площею ділянки всередині еліпса. Це другий закон Кеплера або закон площ. Він передбачив собою пізніше виведений закон збереження моменту імпульсу, на якому ми тут зупинятися не будемо. Висновок з цього закону таке: чим ближче планета до Сонця, тим швидше вона рухається. Здогадуєтеся чому?

Цікаво, що закон площ Кеплер відкрив раніше, ніж форму планетних орбіт. Справа Ви бачите рух комети Галлея навколо Сонця і орбіти планет: Юпітера, Сатурна, Нептуна, Урана і Плутона.

3.
Нарешті, Кеплер відзначився ще й третім законом планетних рухів. Він вирахував, що відносини кубів великих півосей орбіт і квадратів періодів обертання планет навколо Сонця √ величини рівні. або

, Де a 1 і a 2 √ довжини піввісь орбіт двох планет, а T 1 і T 2 √ періоди їх обертання навколо Сонця. Якщо, скажімо, ми знаємо довжину велика піввісь орбіти Землі і період її руху навколо Сонця (рік), то, встановивши з спостережень період руху іншої планети, ми легко можемо обчислити велику піввісь її орбіти. Якщо прийняти велику піввісь Земної орбіту за одиницю, а період обертання вимірювати в роках, то, використовуючи в якості першої планети у формулі третього закону Землю, ми зможемо переписати закон так: a3 = T 2, де а вимірюється в довжинах велика піввісь земної орбіти, а Т √ в роках. Довжину велика піввісь орбіти Землі здавна прийнято називати астрономічної одиницею. Відстань до інших планет в астрономічних одиницях люди дізналися набагато раніше, ніж відстань від Землі до Сонця, завдяки третьому закону Кеплера.

Повторимо, що закони Кеплера √ наслідок його неперевершеного старанності в математичній обробці результатів спостережень. Це √ наглядові закони. Вони відображають закономірності, але не виявляють причин. Після появи закону всесвітнього тяжіння стало очевидним, що закони Кеплера √ лише наслідок фізичного властивості будь-яких тіл, які мають масами, притягатися один одним.

Узагальнений третій закон Кеплера

Закони Кеплера вірні для опису групи тіл, маса одного з яких у багато разів більша за масу інших. У разі Сонячної системи таким потужним тілом є Сонце. Для того щоб, скажімо, описати рух двох близьких один до одного зірок, законів Кеплера загалом слабо. Ньютон зміг ⌠ поправити ■ свого попередника, вивівши третій закон Кеплера для тіл, маси яких треба враховувати. Цей закон називають узагальненим третім законом Кеплера. У нього вже входять значення мас:

За допомогою цього закону можна порівняти рух супутника з масою m 1 навколо тіла з масою M 1 і рух супутника з масою m 2 навколо тіла з масою М 2. Якщо ми обмежимося Сонячною системою, то М 1 = М 2, адже це маса Сонця. Маси всіх інших тіл Сонячної системи малі, в порівнянні з масою Сонця, можна прийняти їх рівними нулю, і Ньютоном закон перетворюється в звичайний третій закон Кеплера.

космічні швидкості

Ньютон пішов набагато далі Кеплера. Він зміг довести що, при досягненні певної швидкості тіло починає рухатися навколо центру обертання не по еліпсу, а по параболі. Ця швидкість цілком залежить від маси центрального тіла і відстані до нього:

Вона називається другою космічною або параболічною швидкістю. Для поверхні Землі ця швидкість дорівнює 11,2 км в секунду. Якщо розігнати ракету до такої швидкості, вона буде рухатися по параболі, а це вже незамкнутая траєкторія. Ракета не стане супутником Землі, а назавжди відійде від неї, ставши супутником Сонця.

Давайте зробимо крок назад від еліпсів, до кругової орбіти. Ту швидкість, яка відповідає кругового руху, називають першою космічною швидкістю. Вона визначається з схожого співвідношення:

Для поверхні Землі перша космічна або кругова швидкість дорівнює 7,9 км в секунду. Діапазон швидкостей між цією величиною і другий космічної відповідає руху тіла по еліпсу.

Нарешті, перевищивши другу космічну швидкість, ми отримуємо гіперболічного траєкторію руху. Зауважте, що в наведених вище формулах (космічні швидкості, закон всесвітнього тяжіння, узагальнений закон Кеплера) відстані відраховуються від центру небесних тіл (Землі, Сонця), а не від їх поверхні. Тому R для поверхні Землі не 0, а приблизно 6 40 0 км.

Для планети і Сонця існує і третя космічна швидкість. Ця швидкість відповідає параболічної швидкості по відношенню до Сонця на відстані радіуса планетної орбіти. Вона дорівнює приблизно 42 км в секунду для Землі. Якщо врахувати, що Земля вже мчить по орбіті, покриваючи за секунду 30 км, то, запускаючи ракету в напрямку руху Землі по орбіті, нам достатньо надати їй швидкість, яка перевищує 12 км в секунду, щоб ця ракета змогла покинути Сонячну систему. Втім, ми можемо і ще виграти в швидкості, якщо згадаємо, що Земля обертається навколо осі. Точки на екваторі нашої планети рухаються найшвидше: майже півкілометра в секунду. Тому, бажаючи зробити найбільш економічний запуск ракети з Землі до зірок, ми повинні були б розташувати стартовий майданчик на екваторі, забезпечити спрямування запуску по дотичній до поверхні, націленої на схід, і натиснути на кнопку пуск опівночі. Спробуйте самі спочатку пояснити собі, чому саме так, а не інакше, а потім ... знайти ту обставину, що ми не врахували, і через якого все вийде зовсім не так.

Отже, ми з'ясували, що всі рухи в Сонячній системі підкоряються закону всесвітнього тяжіння. Виходячи з малої маси планет і тим більше інших тіл Сонячної системи, можна наближено вважати, що руху в околосолнечном просторі підкоряються законам Кеплера. Всі тіла рухаються навколо Сонця по еліптичних орбітах, в одному з фокусів яких знаходиться Сонце. Чим ближче до Сонця небесне тіло, тим швидше його швидкість руху по орбіті (планета Плутон, найдальша з відомих, рухається в 6 разів повільніше Землі). Тіла можуть рухатися і по розімкненим орбітах: параболі або гіперболі. Це трапляється в тому випадку, якщо швидкість тіла дорівнює або перевищує значення другої космічної швидкості для Сонця на даному видаленні від центрального світила. Якщо мова йде про супутнику планети, то і космічну швидкість треба розраховувати щодо маси планети і відстані до її центру.

Зверніться на сторінку про склад Сонячної системи. Ви дізнаєтеся з допомогою неї деякі інші особливості руху планет і інших тіл Сонячної системи, які зовсім не випливають з описаних вище законів