Математична модель розрахунку динаміки двохпозиційних електромагнітних актуаторов вакуумних вимикачів середньої напруги

Наши партнеры ArtmMisto

Математична модель розрахунку динаміки двохпозиційних електромагнітних актуаторов вакуумних вимикачів середньої напруги

Байда Євген Іванович,

кандидат технічних наук, доцент кафедри «Електричні апарати» Харківського національного технічного університету «НТУ ХПІ».

В даний час значний сегмент ринку вимикачів середньої напруги складають вакуумні автоматичні вимикачі [Назарич А. Н.]. За конструкцією приводу такі вимикачі можна класифікувати: вимикачі з пружинно-моторним актуатором і механічної засувкою; вимикачі з електромагнітним актуатором і механічної засувкою; вимикачі з поляризованим бістабільності актуатором, у якого роль механічної засувки виконує висококоерцитівниє постійний магніт.

Останній тип актуаторов широко використовується фірмою АББ [Вакуумний вимикач VM1] і має ряд істотних переваг (простота і надійність конструкції) в порівнянні з іншими типами (рис.1).

Мал. 1. Поляризований двохпозиційний актуатор.

Такий актуатор запатентований фірмою АББ і складний у виробництві. У зв'язку з цим були запропоновані альтернативні конструкції актуаторов [Бугайчук В.М., Клименко Б.В.], показані на рис. 2 в циліндричній системі координат.

а) б)

Мал. 2. Двопозиційні бістабільні поляризовані актуатори: а) асиметричний актуатор з зовнішнім якорем; б) симетричний актуатор з внутрішнім якорем.

Утримання якоря в кінцевих положеннях здійснюється за рахунок енергії постійних магнітів, а напруга на котушки подається на короткий час для зміни положення якоря.

При проектуванні такого роду пристроїв недостатньо проведення тільки статичних розрахунків. Основними є динамічні методи розрахунку, що дозволяють детально розібратися в фізиці процесів, що відбуваються і зробити остаточний висновок про працездатність конструкції. Розрахунки такого роду можуть бути проведені тільки на підставі відповідних математичних моделей, в основі яких лежать рівняння електромагнітного поля, рівняння електричного кола і рівняння руху [Байда Є.І.]. Складність полягає в необхідності проведення розрахунків електромагнітного поля в неоднорідній, нелінійної, проводить або непроводящей середовищі з урахуванням руху розрахункових областей і наявності постійних магнітів.

Метою даної статті є опис математичної моделі розрахунку динаміки поляризованого бістабільності актуатора, побудованого на базі висококоерцитівниє постійних магнітів.

Розрахункові рівняння низькочастотного електромагнітного поля.

1. Нерухома частина муздрамтеатру:

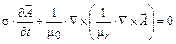, (1)

де s - провідність; 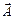- векторний магнітний потенціал; m r = m r (|| B ||) - відносна магнітна проникність.

2. Рухома частина муздрамтеатру (якір):

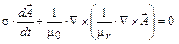. (2)

Перетворимо отримане вираження за допомогою співвідношень векторної алгебри [Френкель Я.І. ]:

,

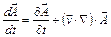але

,

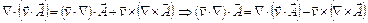де 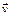- швидкість руху якоря.

Так як швидкість руху якоря залежить тільки від часу і не залежить від координат, то:

,

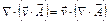але

,

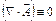тому

.

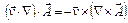Отже, в остаточному варіанті розрахункове рівняння запишеться:

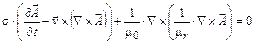. (3)

3. Котушки електромагніта можна вважати «поганим» немагнітним провідником з щільністю струму, що визначається сторонніми джерелами:

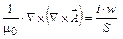, (4)

де i - струм котушки; w - число витків котушки; S - перетин котушки.

4. Область постійного магніту можна уявити як провідну нерухому середовище, що має апріорі задану намагніченість, тоді:

,

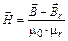де 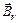- залишкова магнітна індукція.

В цьому випадку:

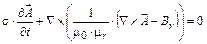. (5)

5. Рівняння для середовища, що оточує магніт:

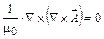. (6)

У розрахунках електромагнітних систем досить часто значення поля не є метою розрахунку. Як правило, необхідно визначити значення електромагнітних сил, що діють на одну з частин системи. Для цього необхідно скористатися найбільш універсальною формулою - тензором натягу Максвелла:

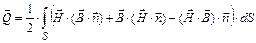, (7)

де 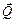- значення електромагнітної сили; 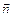- вектор зовнішньої нормалі до поверхні інтегрування .

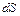Система рівнянь (1-7) повинна бути доповнена початковим і граничними умовами (умова аксиальной симетрії і значенням поля на кордоні розрахункової області).

Розрахункові рівняння електричного кола.

У рівнянні (4) присутній щільність струму сторонніх джерел, яка визначається рівнянням електричного кола. Рівняння електричного кола для котушки електромагніта:

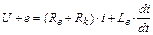, (8)

де U - напруга джерела; e - протівоедс, що наводиться в котушці; Re - активний опір зовнішнього ланцюга; Rk - активний опір котушки; i - струм котушки; Le - індуктивність зовнішньої ланцюга.

Необхідно відзначити, що джерелом напруги може бути постійна напруга, випрямлена змінну напругу або попередньо заряджений конденсатор. Тому:

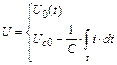, (9)

де U0 (t) - постійне, або випрямлена напруга; Uс0 - початкова напруга на конденсаторі; С - ємність конденсатора.

Що стосується значення протівоедс, то відповідно до закону Фарадея:

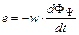, (10)

де w - число витків котушки; F Y - потік, наведений по потокозчеплення, тобто потік, пов'язаний з усіма витками котушки.

Визначимо цей потік в такий спосіб:

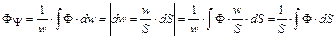, (11)

де F - магнітний потік, охоплений витками котушки; S - площа поперечного перерізу котушки.

Згідно з теоремою Стокса, зв'язок між потоком векторного поля через орієнтовану поверхню і циркуляцією цього поля по краю поверхні, можна представити у вигляді:

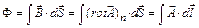, (12)

де 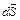- площа, пронизує магнітним потоком; - напрямок обходу контуру циркуляції вектора .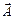

Отже, формулу (10) з урахуванням (11-12) можна уявити:

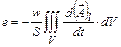, (13)

де 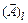- проекція векторного магнітного потенціалу на напрям обходу контуру; V - об'єм котушки.

Остаточно розрахункове рівняння для електричного кола запишеться у вигляді з урахуванням (9):

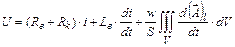. (14)

Початкові умови для рівняння (14) нульові.

Рівняння механічної ланцюга.

Конструкція приводу вакуумного вимикача є багатоланковим механізм, при розрахунках якого необхідно враховувати інерційність всіх рухомих частин. Основним є рівняння руху якоря електромагніту:

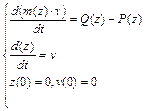, (15)

де 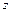- переміщення якоря; - швидкість якоря; 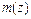- маса рухомих частин, наведена до якоря; - швидкість якоря; - електромагнітна сила; 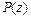- протидіюча сила, наведена до якоря.

Рівняння (15) являє собою рівняння одновимірного руху зі змінною масою. Для зручності розрахунків воно може бути переписано у вигляді:

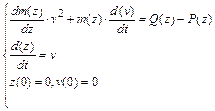. (16)

Отримані рівняння (1-16) представляють собою систему рівнянь і є математичною моделлю динаміки розглянутих актуаторов (рис. 2). На підставі рівнянь (1-16) може бути отримано рішення широкого кола завдань, таких як розрахунки индукционно - динамічних систем, магнітно імпульсної обробки матеріалів і т.п.

Отримати рішення рівнянь (1-16) досить складно, так як виникають проблеми з точністю, сходимостью і стійкістю системи.

Рішення системи (1-16) було отримано з використанням методу скінченних елементів для інтегрування по просторовим змінним і вдосконаленого методу Гіра, званого BDF (Backward Differentiation Formula) [Ракитский Ю.В. ] по часу. При інтегруванні системи необхідно уникати стрибкоподібного зміни параметрів (наприклад, зміна приведеної маси при замиканні головних контактів). У цьому випадку необхідна апроксимація переходу безперервної гладкою (аж до другої похідної) функцією (рис. 3), при використанні якої стрибок функції «розмивається» на певному просторовому або часовому інтервалі.

Мал. 3. Приклад апроксимації зміни маси.

Спочатку метод кінцевих елементів був погано пристосований для вирішення нестаціонарних задач [Мітчелл Е., Сегерлінд Л., Сильвестр П.]. Рішенням даної проблеми є використання «деформованої» сітки. Суть методу полягає в тому, що рухливі області представляються розташованими в деякому еластичному просторі, покритому сіткою. При зміні положення області, сітка, що належить області залишається незмінною, а координати сітки, що належать кордонів рухливих областей, зазнають деформацію відповідно до заданого законом руху, що визначається рівнянням (16) (рис. 4).

а) б)

Мал. 4. Деформація сітки: а) вихідна сітка; б) деформована сітка.

З теорії методу скінченних елементів відомо [Мітчелл Е., Сегерлінд Л., Сильвестр П.], що розмір і форма осередків сітки істотно впливають на точність розрахунків, тому при русі області на кожному часовому кроці необхідно перевіряти «якість» сітки, перебудовуючи сітку по міру необхідності.

На підставі викладеного матеріалу були проведені розрахунки динаміки актуаторов, деякі результати яких показані на рис. 5.

Мал. 5. Розрахунок магнітної індукції і вихрових струмів при включенні актуатора: а) модуль магнітної індукції в моменти часу 2 мс, 20 мс, 33 мс .; б) вихровий струм муздрамтеатру в моменти часу 2 мс, 20 мс, 33 мс.

висновки

За розробленої математичної моделі були проведені розрахунки динаміки бістабільних актуаторов на базі висококоерцитівниє постійних магнітів, що дозволили створити працездатні конструкції актуаторов відповідно до вимог технічного завдання.

література

1. Байда Є.І. Розрахунок перехідних процесів в електромагнітному механізмі на підставі рівнянь електромагнітного поля / Є.І. Байда Електротехніка та електромеханіка. - Харків: НТУ «ХПІ», 20008. - №6. С.-39-43.

2. Байда Є.І. Вплив провідності матеріалу на динамічні характеристики електромагнітних механізмів постійного струму / Є.І. Байда Електротехніка та електромеханіка. - Харків: НТУ «ХПІ», 2010. - №1. С.-3-5.

3. Байда Є.І. Моделювання динамічних характеристик електромагнітних механізмів постійного струму з магнітною клямкою / Є.І. Байда Електротехніка та електромеханіка. - Харків: НТУ «ХПІ», 2010. - №2. С.-3-5.

4. Байда Є.І. Моделювання процесу відключення електромагніту постійного струму з магнітною клямкою / Є.І. Байда Електротехніка та електромеханіка. - Харків: НТУ «ХПІ», 2010. - №3. С.-6-9.

5. Байда Є.І. Розрахунок динаміки двохпозиційного електромагніту постійного струму з магнітною клямкою / Є.І. Байда Електротехніка та електромеханіка. - Харків: НТУ «ХПІ», 2010. - №4. С.-10-12.

6. Байда Є.І. Вплив форми напруги джерела живлення на динамічні характеристики електромагніта постійного струму / Є.І. Байда Електротехніка та електромеханіка. - Харків: НТУ «ХПІ», 2010. - №5. С.-3-4.

7. Байда Є.І. Математичні моделі підключення джерел бістабільних поляризованих актуаторов до джерел енергііенергіі / Є.І. Байда Вісник національного технічного університету «Харківський політехнічний інститут». - Харків: НТУ «ХПІ», 2012. - №49.

8. Бугайчук В.М. Обгрунтування доцільності використання обмоток включення і відключення бістабільних електромагнітних приводах вакуумних вимикачів / Бугайчук В.М. , Клименко Б.В., Ємельянов В.Л. Електротехніка и електромеханіка - 2011. - №3. - С. 21 - 24.

9. Вакуумний вимикач VM1 з електромагнітним приводом [Електронний ресурс] - Режим доступу: http://www05.abb.com/ .

10. Клименко Б.В. Електромагнітні приводи вакуумних вимикачів середніх напружень / Б.В. Клименко, В.М. Бугайчук, А.М. Гречко Вісник НТУ «ХПІ». - 2004. - № 42. - С. 73 - 80.

11. Клименко Б.В. Дослідний зразок двохпозиційного електромагнітного приводу вакуумного вимикача середньої напруги / Клименко Б.В., Гречко А.М., Бугайчук В.М. Електротехніка и електромеханіка - 2005. - №2. - С. 23 - 28.

12. Клименко Б.В. Швидкодіючий електромагнітний привід з витісненням магнітного поля для вакуумного вимикача середньої напруги / Клименко Б.В., Гречко А.М., Бугайчук В.М., Вировець С.В. Електротехніка и електромеханіка - 2006. - №4. - С. 22 - 26.

13. Клименко Б.В. Електромагнітний привід з двохпозиційної магнітною засувкою для вакуумного вимикача середньої напруги / Клименко Б.В., Гречко А.М., Єресько О.В. Електротехніка и електромеханіка - 2007. - №6. - С. 40 - 43.

14. Мітчелл Е. Метод кінцевих елементів для рівнянь з приватними похідними / Е. Мітчелл, Р. Уейт. - М .: Світ, 1981. - 216 с.

15. Назарич А. Н. Аналіз основних переваг вакуумних вимикачів. [Електронний ресурс] / Назарич А. Н. БЕСТЕР Комплект. - Режим доступу до журн .: http://www.bester54.ru/cms.php?type=page&id=22 .

16. Ракитский Ю.В. Чисельні методи рішення жорстких систем / Ракитский Ю.В., Устинов CM, Черноруцкий І.Г. - M .: Hаука, 1979.

17. Сегерлінд Л. Застосування методу кінцевих елементів / Сегерлінд Л. - М .: Світ, 1979. - 392 с.

18. Сильвестр П. Метод кінцевих елементів для радіоінженерів і інженерів електриків / П. Сильвестр, Р. Феррарі. - М .: Світ, 1986. - 229 с.

19. Френкель Я.І. Курс теоретичної механіки / Френкель Я.І. - Ленінград: Друкарня «Червоний друкар», 1939. - 386 с.

Надійшла до редакції 14.01.2013 р